Extreme Learning Machines

Artificial neural networks are a common technique in the field of machine learning. Inspired by biology, they are used in, among others, function approximation, time series prediction, classification and pattern recognition. There exist many variations in the type of network, the types of neurons used, and in the learning algorithms. The most common learning algorithm for a feedforward neural network is backpropagation.

Although the backpropagation algorithm is a very popular learning algorithm, there are some drawbacks:

• A small learning rate can lead to slow convergence.
• A large learning rate can lead to divergence.
• The algorithm might get stuck at local minima.
• It is possible to overtrain the network, reducing the generalisation performance.
• The algorithm can be very time-consuming, especially for large networks.

In 2004, a new alternative to backpropagation for learning feedforward neural networks has been proposed by Huang: Extreme Learning Machine (ELM). This algorithm is easy to implement and does not suffer from the drawbacks above. I will first show a summary of the theory behind this algorithm, and then provide a supervised learning example implemented in MATLAB.

Note that this technique is very similar to Reservoir Computing techniques for recurrent neural networks. See Remco’s blog about Echo State Networks for a description.

Theory

Suppose we want to train a feedforward neural network with one hidden layer in a supervised learning setting by providing input \(x\) and desired output \(y\). If the hidden layer contains synaptic weights \(SH\) and bias \(BH\) and the hyperbolic tangent as a sigmoid activation function, the output \(H\) of the hidden layer can be computed as \(H = tanh(-BH + SH*x)\).

For the output layer, we use a linear activation function (though we could also use a sigmoid function here) and weights \(S\) and no bias. Then the output \(O\) of the whole neural network can be computed as \(O = S*H\).

Now we want the neural network to produce an output \(O\) that minimizes the error \(||y-O||\), given input data \(x\). In the backpropagation algorithm this is done by performing a gradient descent on the error to update the hidden weights \(S*H\) and the output weights \(S\). In the ELM approach, however, the hidden weights are initialised randomly and remain fixed; only the output weights are adapted.

Suppose the weights and biases of the hidden layer are fixed, then we can compute the outputs of the hidden layer for all the training samples at once. This gives a matrix \(\bf{H}\) of dimension \(h*T\), where \(h\) is the amount of hidden neurons and \(T\) the amount of training samples. Since the desired output \(y\) is also known for all the training samples, for the network to produce the desired output we need to solve the linear matrix equation \(S*\bf{H} = y\). This equation does not necessarily have an exact solution, but the best (smallest norm least-squares) solution of this equation is \(S = y*\bf{H^+}\), where \(\bf{H^+}\) is the Moore-Penrose pseudo-inverse of \(\bf{H}\). Even with fixed weights going from input to hidden layer, using this \(S\) for the output weights gives good results in theory and in practice. For more information, see Huang, Guang-Bin, Qin-Yu Zhu, and Chee-Kheong Siew. “Extreme learning machine: theory and applications.” Neurocomputing 70.1 (2006): 489-501.

Practice

The above approach is easy to implement in MATLAB, or in any environment that can handle a pseudo-inverse (or you can implement a pseudo-inverse yourself). Here, an example is shown to let a feedforward neural network with one hidden layer learn the XOR function.

First, set the amount of training and generalisation samples and the input and output dimensions:

T = 100; %amount of
training samples gen = round(0.2*T); %amount of generalisation samples id = 2;
%input dimension od = 1; %output dimension 

For the input, random values from the set \(\{0,1\}^2\) are picked. And since the function we want to learn is actually a known function, we can easily compute the desired output values:

x = round(rand(id,T+gen));
%input data y = zeros(od,T+gen); %output data for t=1:T+gen y(:,t) =
xor(x(1,t),x(2,t)); %function to be learned end 

Of course, in a more realistic application \(y\) might not be given as a function of \(x\) so easily, since that is exactly what the neural network needs to learn. But in this example the function to be learned is known explicitly. We also know the different possible values of the input data, so only 4 hidden nodes will suffice for the network. In practice, one might need to find the amount of hidden nodes just by trial and error or by using an incremental algorithm.

Initialise the neural network:

h = 4; %amount of hidden nodes
SH = rand(h,id); %input-to-hidden synaptic weights, fixed
BH = rand(h,1)*ones(1,T+gen); %hidden layer bias, fixed
S = zeros(od,h); %hidden-to-output synaptic weights, to be adapted 

The hidden layer bias and weights will be fixed during the whole algorithm, while the output weights will be adapted. It is important that the randomly initialised weights and biases are drawn from a continuous probability distribution, but it does not matter which one.

The outputs of the hidden layer can be computed for every training sample:

H = tanh(-BH + SH*x); %Calculate hidden layer output matrix

When using your own inputs and outputs, sometimes the outputs of the hidden layer will all be 1 or -1, or close to it. This could give problems in the learning phase. You can try to normalise the input or the weights and biases in this case.

The learning phase is now only one line of code:

S = y(:,1:T)*pinv(H(:,1:T)); %adjust hidden-to-output synaptic weights during learning phase

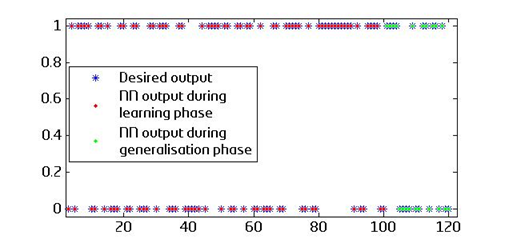
Only the output weights are adapted, the hidden weights remain fixed. The neural network has now learned the XOR function in one step, by only adapting the output weights. The next code can be used to visualise this:

O = S*H; %output
plot(y,'b*'); %desired output hold on;
plot(1:T,O(:,1:T),'r.'); %output during learning phase
hold on; plot(T+1:T+gen,O(:,T+1:T+gen),'g.'); %output during generalisation phase
hold off;